Skip to main content

树 Tree

基本概念​

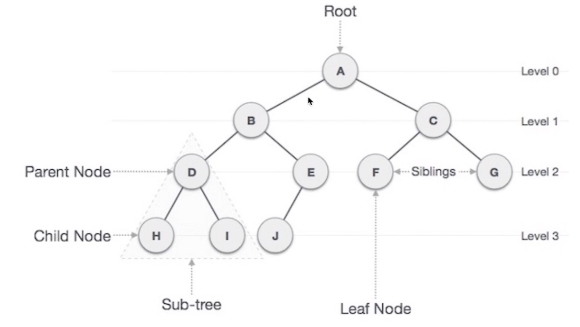
  • Root: 起源节点
  • Leaf: 叶子节点
  • Child Node: 子节点
  • Parent Node: 父节点
  • Left/Right Node: 左/右节点
  • Edge: 边, 连线
  • Subtree: 子树
  • Height: 节点到 leaf 节点 edge 的数量，例如 B 的 Height 是 2
  • Depth: 节点到 root 节点 edge 的数量，例如 B 的 Depth 是 1

分类​

  • 二叉树 (Binary Tree): 每个节点最多包涵两个子节点，上面图示中的树就是二叉树。
  • 满二叉树 (Full Binary Tree): 在满二叉树中，每个不是尾节点的节点都有两个子节点。
  • 完全二叉树 (Complete Binary Tree): 假设一个二叉树深度 (depth) 为 d (d>1)，除了第 d 层外，其他隔层的数量均已达到最大值，且第 d 层所有节点从左向右紧密排列，这样的二叉树就是完全二叉树。
  • 排序二叉树 (Binary Search Tree): 在此树中，每个节点的数值比左子树上的节点都大，比所有右子树上的节点都小。
  • 平衡二叉树 (AVL Tree): 任何节点的两颗子树的高度差不大于 1 的排序二叉树。
  • B 树 (B-Tree): B 树和平衡二叉树一样，只不过它是一种多叉树 (一个节点的子节点数量可以超过 2)。
  • 红黑树 (Red-Black Tree): 是一种自平衡二叉树寻找树。

排序二叉树 Binary Search Tree​

Java Implementation 代码实现​

public class BST {
    static class TreeNode {
        public int value;
        public TreeNode left;
        public TreeNode right;
        public TreeNode (int value) {
            this.value = value;
        }
    }

    private TreeNode root;

    public TreeNode get(int key) {
        TreeNode current = root;
        while (current != null && current.value != key) {
            if (key < current.value) {
                current = current.left;
            } else if (key > current.value) {
                current = current.right;
            }
        }
        return current == null ? null : current;
    }

    public void insert (int key) {
        if(root == null) {
            root = new TreeNode(key);
            return;
        }
        TreeNode current = root;
        TreeNode parent = null;
        while (true) {
            parrent = current;
            if(key < parent.value>) {
                current = parent.left;
                if (current == null) {
                    parent.left = new TreeNode(key);
                    return ;
                }
            } else if (key > Parent.value) {
                current = parent.right;
                if (current == null) {
                    parent.right = new TreeNode(key);
                    return;
                }
            } else {
                return ; // BST does not allow nodes with the same value
            }
        }
    }

    public boolean delete (int key) {
        TreeNode parent = root;
        TreeNode current = root;
        boolean isLeftChild = false;

        while (current != null && current.value != key) {
            parent = current;
            if(current.value > key) {
                isLeftChild = true;
                current = current.left;
            } else {
                isLeftChild = false;
                current = current.right;
            }
        }

        if (current == null) {
            return false;
        }

        // Case 1: if node to be deleted as no children
        if(current.left == null && current.right == null) {
            if (current == root) {
                root = null
            } else if (isLeftChild) {
                parent.left = null;
            } else {
                parent.right = null;
            }
        }

        // Case 2: if node to be deleted has only one child
    } else if (current.right == null) {
        if (current == root) {
            root = null;
        } else if(isLeftChild) {
            parent.left = current.left;
        } else {
            parent.right = current.left;
        }
    } else if (current left == null) {
        if (current == root) {
            root = null;
        } else if (isLeftChild) {
            parent.left = current.right;
        } else {
            parent.right = current.right;
        }
    // Case 3: current.left != null && current.right != null
    } else {
        const successor = this.getMinSuccessorAtRightSubTree(current);
        if(current == root) {
            root = null;
        } else if (isLeftChild) {
            parent.right = successor;
        } else {
            parent.left = successor;
        }
        successor.left = current.left;
    }
    return true;

    private TreeNode getMinSuccessorAtRightSubTree (Treenode node) {
        TreeNode successorParent = null;
        TreeNode successor = null;
        TreeNode current = node.right;
        while (current != null) {
            successorParent = successor;
            successor = current;
            current = current.left;
        }
        if(successor != node.right) {
            successorParent.left = successor.right;
            successor.right = node.right;
        }
        return successor;
    }
}

Tree Traversal​

  • Pre-order Traversal: 先访问节点自己，然后访问左子树，最后访问右子树
  • In-order Traversal: 先访问左子树上的节点，然后访问自己，最后访问右子树上的节点
  • Post-order Traversal: 先访问左右子树，最后再访问自己

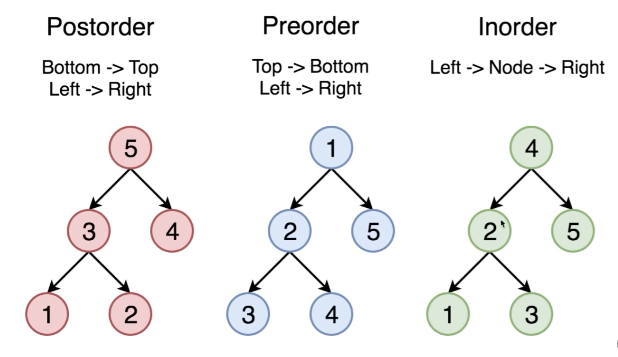
Combination: Binary Search Tree + In-order Traversal

Pre-order Traversal Implementation​

public static void preOrderTraversal (TreeNode root) {
    if (root == null) {
        return;
    }
    System.out.println(root.value);
    preOrderTraversal(root.left);
    preOrderTraversal(root.right);
}

In-order Traversal Implementation​

public static void inOrderTraversal (TreeNode root) {
    if (root == null) {
        return;
    }
    inOrderTraversal(root.left);
    System.out.println(root.value);
    inOrderTraversal(root.right);
}

Post-order Traversal Implementation​

public static void postOrderTraversal (TreeNode root) {
    if (root == null) {
        return;
    }
    postOrderTraversal(root.left);
    postOrderTraversal(root.right);
    System.out.println(root.value);
}

来源​