Skip to main content

优先队列 PriorityQueue, 堆 Heap

优先队列 PriorityQueue​

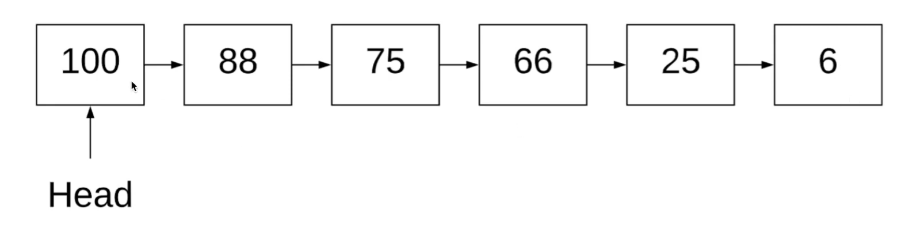
类似链表，由多个节点组成。

  • push: 插入一个新的元素
  • pop: 将优先级最高的元素弹出 (删除)
  • peek: 查看优先级最高的元素数值
  • isEmpty

Java Implementation​

public class PriorityQueue {
    static class Node {
        int value;
        int priority;
        Node next;

        public Node (int value, int priority) {
            this.value = value;
            this.priority = priority;
        }
    }

    Node head = null;

    // push 方法的时间复杂度是 O(n)， 仍可以进行优化
    public void push (int value, int priority) {
        if (head == null) {
            head = new Node(value, priority);
            return;
        }
        Node current = head;
        Node newNode = new Node(value, priority);
        if (head.priority < priority) {
            newNode.next = head;
            head = newNode;
        } else {
            while (current.next != null && current.next.priority > priority ) {
                current = current.next;
            }
            newNode.next = current.next;
            current.next = newNode;
        }
    }

    public Node peek() {
        return head;
    }

    public Node pop() {
        if (head == null) {
            return null;
        }
        Node temp = head;
        head = head.next;
        return temp
    }

    public booelan isEmpty() {
        return head == null;
    }
}

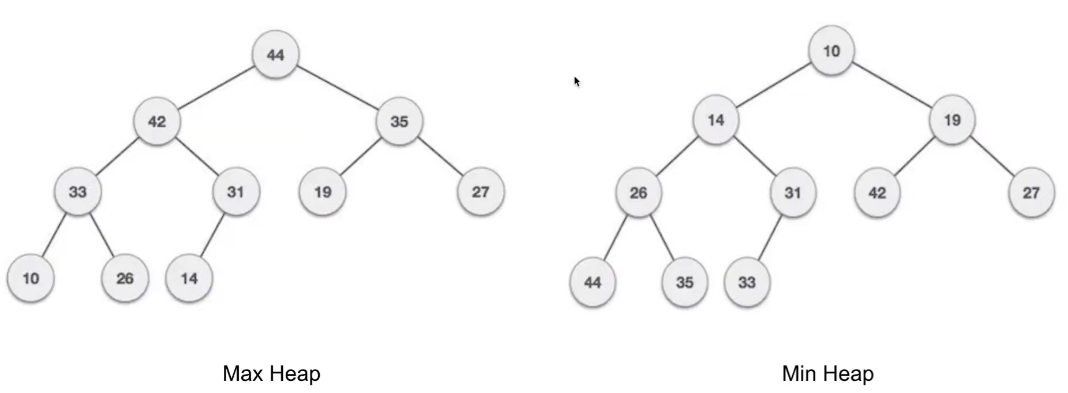
堆 Heap​

Heap 属于完全二叉树 (Complete Binary Tree)。

  • insert: 将新元素插入堆
  • poll: 将根节点 (数值最大的元素) 删除
  • peek: 获取根节点的数值

实现思路​

插入 insert​

  1. 在堆的最后新建一个节点。
  2. 将数值赋予新节点。
  3. 将新节点和父节点比较。
  4. 如果新节点的数值比父节点大，调换父子节点的位置。
  5. 重复步骤 3 和 4 指导最大堆的特性被满足

移除 poll​

  1. 移除根节点
  2. 将最后的元素移到根节点处
  3. 将子节点和父节点比较。
  4. 如果父节点的数值与较大的子节点的数值对比，父节点比较小的话，调换父子节点的位置。
  5. 重复步骤 3 和 4 指导最大堆的特性被满足

Java Implementation​

public class MaxHeap {
    private int capacity;
    private int size = 0;
    private int[] array;

    public MaxHeap(int capacity) {
        this.capacity = capacity;
        this.array = new int[capacity];
    }

    private int getLeftChildIndex(int parentIndex) {
        return 2 * parentIndex + 1;
    }

    private int getRightChildIndex(int parentIndex) {
        return 2 * parentIndex + 2;
    }

    private int getParentIndex(int childIndex) {
        return (childIndex-1)/2;
    }

    private boolean hasLeftChild(int index) {
        return getLeftChildIndex(index) < size;
    }

    private boolean hasRightChild(int index) {
        return getRightChildIndex(index) < size;
    }

    private boolean hasParent(int index) {
        return getParentIndex(index) < size;
    }

    private int leftChild(int parentIndex) {
        return array[getLeftChildIndex(parentIndex)];
    }

    private int rightChild(int parentIndex) {
        return array[getRightCHildIndex(parentIndex)];
    }

    private int parent(int childIndex) {
        return array[getParentIndex(childIndex)];
    }

    public void insert(int item) { // Time Complexity: O(logN)
        if (size == capacity) {
            array = Array.copyOf(array, capacity * 2);
            capacity = capacity * 2;
        }
        array[size] = item;
        size++;
        heapifyUp();
    }

    private void heapifyUp() {
        int index = size - 1;
        while(hasParent(index) && parent(index) < array[index]) {
            swap(getParentIndex(index), index);
            index = getParentIndex(index);
        }
    }
    private void swap(index_1, index_2) {
        int tmp = array[index_1];
        array[index_1] = array[index_2];
        array[index_2] = tmp;
    }

    public void poll() { // Time Complexity: O(logN)
        if(size == 0) {
            throw new NoSuchElementException();
        }
        int element = array[0];
        array[0] = array[size-1];
        size--;
        heapifyDown();
    }

    private void heapifyDown() {
        int index = 0;
        while(hasLeftChild(index)) { // Because of the feature of Complete Binary Tree
            int largerChildIndex = getLeftChildIndex(idnex);
            if(hasRightChild(index) && rightChild(index) > leftChild(index)) {
                largerChildIndex = getRightChildIndex(index);
            }
            if(array[index] < array[largerChildIndex]) {
                swap(index, largerChildIndex);
            } else {
                break;
            }
            index = largerChildIndex;
        }
    }

    private int peek() {
        if (size == 0) {
            throw new NoSuchElementException();
        }
        return array[0];
    }
}

来源​