Skip to main content

图 Graph

图 Graph​

  • Vertice: 顶点
  • Edge: 相连线

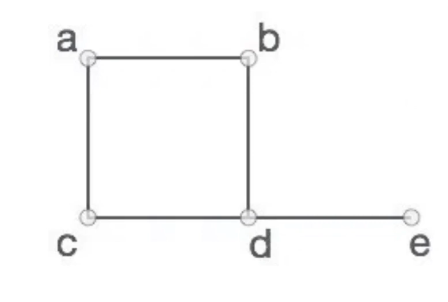
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}

种类​

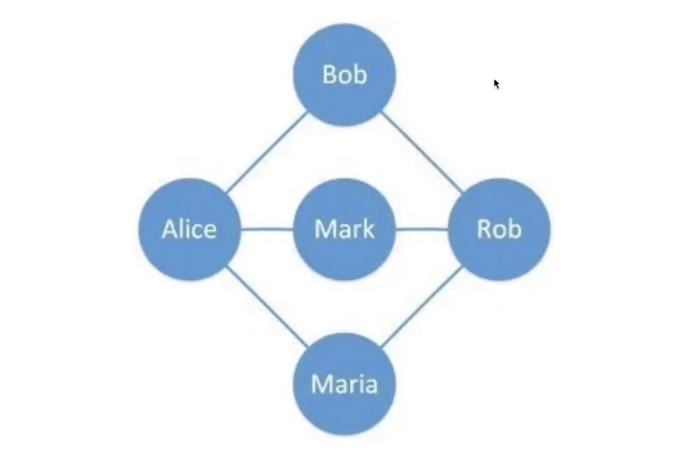
  • 无向图 (Undirected Graph): 在无向图中，每个顶点和其他顶点通过连接线连接。
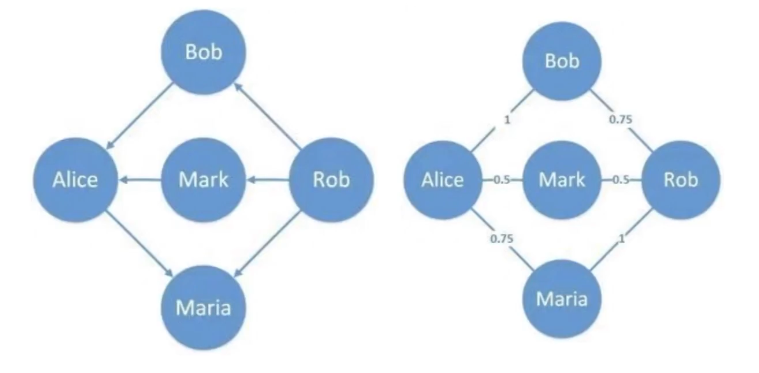
  • 有向图 (Directed Graph): 有向图中的相连线是有方向的。
  • 权重图 (Weighted Graph): 在权重图中，每条相连线有各自的权重。

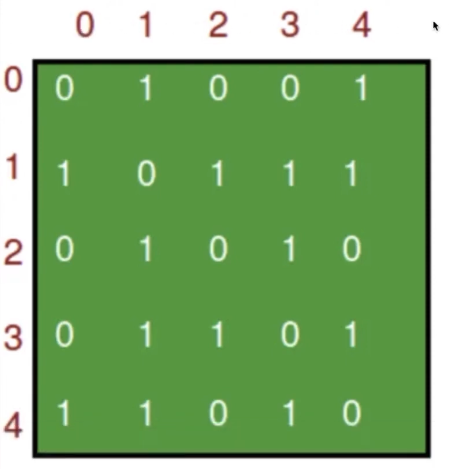
有向图的实现 (矩阵)​

查询很方便
空间复杂度很糟糕

if M[i][j] == 1 => i -> j

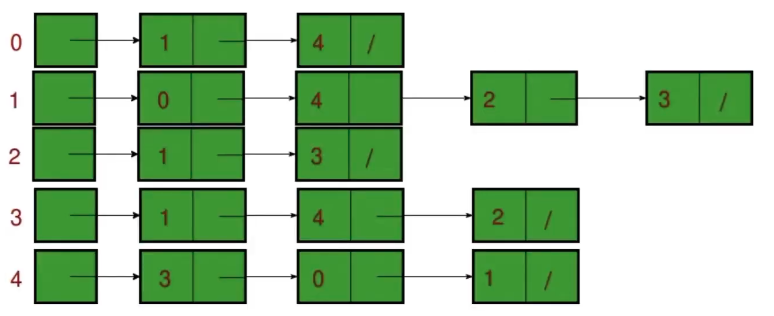
有向图的实现 (链表)​

只记录有意义的数据，那些存在的相连线。

Java Implementation​

public class ListGraph {
    // ArrayList<ArrayList<Integer>> 在概念上可以被看作是一个链表的链表，实际上它更类似于数组的数组，即一个动态重新分配的数组。
    ArrayList<ArrayList<Integer>> graphs;

    public ListGraph(int v) {
        graphs = newArrayList<>(v);
        for (int i=0; i<v; i++) {
            graphs.add(newArrayList<>());
        }
    })

    public void addEdge(int start, int end) {
        graphs.get(start).add(end);
    }

    public void removeEdge(int start, int end) {
        graphs.get(start).remove((Integer)end)
    }
}

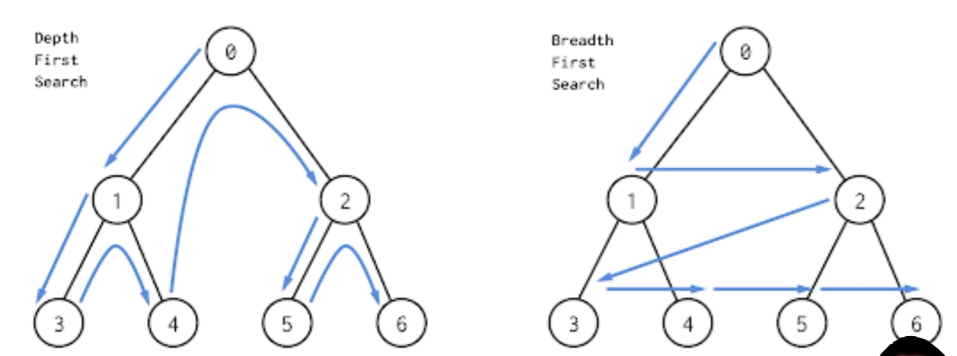
图的遍历 (Graph Traversal)​

Java Implementation

public class GraphTraversal {
    ListGraph graph;
    boolean[] visited;

    public GraphTraversal(ListGraph listGraph) {
        this.graph = listGraph;
        visited = new boolean[listGraph.graphs.size()];
    }
    ...
}

Java Implementation

public void DFS() {
    for(int i=0; i<graph.graphs.size(); i++) {
        if(!visited[i]) {
            DFSTraversal(i);
        }
    }
}
public void DFSTraversal(int v) {
    if(visited[v]) return;
    visited[v] = true;
    Systsem.out.print(v + "->");
    Iterator<Integer> neighbors = graph.graphs.get(v).listIterator();
    while(neigbors.hasNext()) {
        int nextNode = neighbors.next();
        if(!visited[nextNode]) {
            DFSTraversal(nextNode);
        }
    }
}

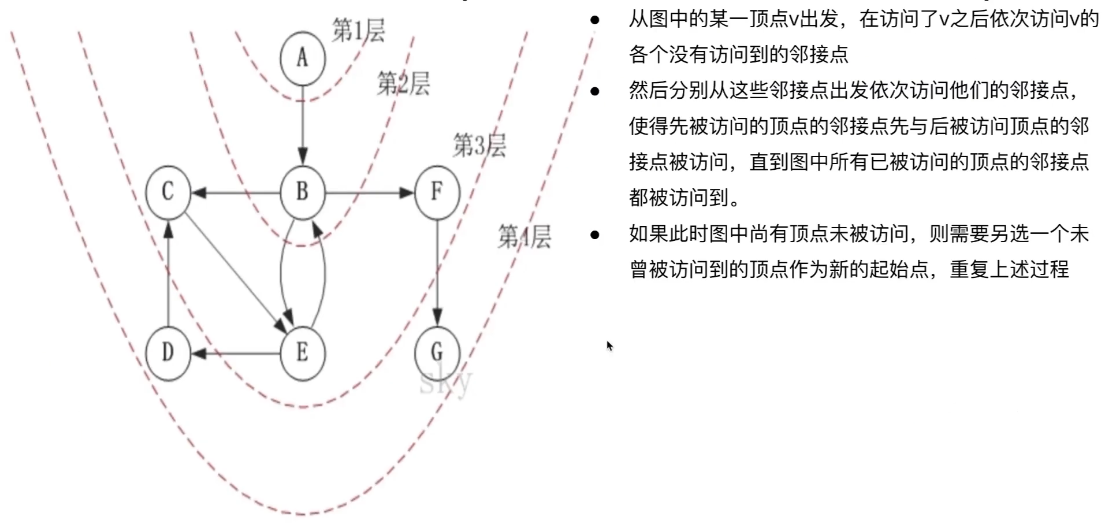
public void BFS() {
    for(int i=0; i<graph.graphs.size(); i++) {
        if(!visited[i]) {
            BFSTraversal(i);
        }
    }
}
public void BFSTraversal(int v) {
    Deque<Integer> queue = new ArrayDeque<>();
    visited[v] = true;
    queue.offerFirst(v);
    while(queue.size != 0) {
        integer cur = queue.pollFirst();
        Systsem.out.print(cur + "->");
        Iterator<Integer> neighbors = graph.graphs.get(cur).listIterator();
        wihle(neighbors.hasNext()) {
            int nextNode = neighbors.next();
            if(!visited[nextNode]) {
                queue.offerLast(nextNode);
                visited[nextNode] = true;
            }
        }
    }
}

来源​