Skip to main content

排序算法

  1. 插入排序 Insertion Sort
  2. 快排 Quick Sort
  3. 归并排序 Merge Sort

插入排序 Insertion Sort​

在插入排序中，我们从前到后依次处理未排好序的元素，对于每个元素，我们将它与之前排好序的元素进行比较，找到对应的位置后并插入。

High Level Think​

  1. 从第二个元素 (第一个要被排序的新元素) 开始，从后向前扫描之前的元素序列
  2. 如果当前扫描的元素大于新元素，将扫描元素移动到下一位
  3. 重复步骤 2，直到找到一个小于或者等于新元素的位置
  4. 将新元素插入到该位置
  5. 对于之后的元素重复步骤 1 ～ 4
Pseudocode
function insertion_sort(array[]):
    // i 的位置就是新元素的位置
    for (i=1; i < array.length; i++):
        cur = array[i]
        j = i - 1
        while (j >= 0 && array[j] > cur):
            array[j+1] = array[j]; // 将 j 位置的元素赋值给 j+1 位置
            j--; // j 向左移动一个位置
        array[j+1] = cur

代码​

public void insertionSort(int[] array) {
    for (int i=1; i < array.length; i++) {
        int cur = array[i];
        int insertionIndex = i - 1;
        while (insertionIndex >= 0 && array[insertionIndex] > cur) {
            array[insertionIndex + 1] = array[insertionIndex];
            insertionIndex--;
        }
        array[insertionIndex + 1] = cur;
    }
}

复杂度分析​

时间复杂度: O(n^2)
空间复杂度: O(1)

快排 Quick Sort​

快排是一种分治 (Divide and Conquer) 算法，在这种算法中，我们把大问题变成小问题，然后将小问题逐个解决，当小问题解决完时，大问题迎刃而解。

选中一个目标元素，然后将目标元素放到数组中正确的位置。然后根据排好序后的元素，将数组分为两个子数组，用相同的方法，在没有排好序的范围使用相同的操作。

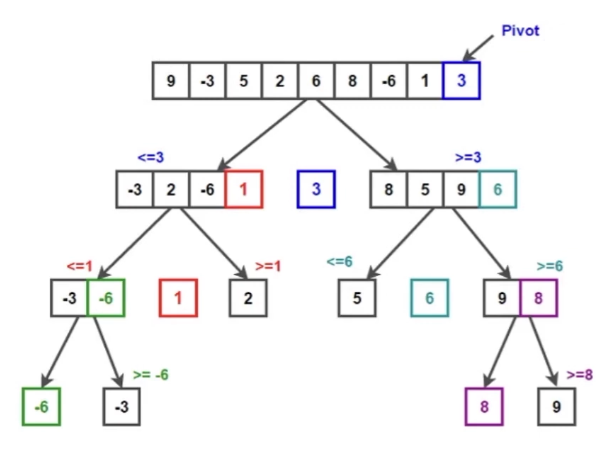
High Level Think​

  1. 对于当前的数组，取最后一个元素当作基准数 (pivot)
  2. 将所有比基准数小的元素排到基准数钱，比基准数大的排在基准数之后
  3. 当基准数被放到准确的位置之后，根据基准数数的位置将数组切分为前后两个子数组
  4. 对字数组采用步骤 1 ～ 4 的递归操作，直至子数组的长度小于等于 1 为止
Pseudocode
function quickSort (array: number[], left, right):
    if(left >= right) return;
    // 找到一个 pivot 位置
    partitionIndex = partition(array, left, right)
    quickSort(array, left, partitionIndex - 1)
    quickSort(array, partitionIndex + 1, right)

function partition (array: number[], left, right):
    pivot = array[right]
    smallerElementIndex = left
    biggerElementIndex = right - 1
    while(true):
        // 从 left 往 right 找，知道找到一个比当前 pivot 大的数
        while (smallerElementIndex < right && array[smallerElementIndex] <= pivot):
            smallerElmentIndex++;
        // 从 right - 1 往 left 找，知道找到一个比当前 pivot(right) 小于或等于 的数
        while (biggerElemnentIndex >= left && array[biggerElmentIndex] > pivot):
            biggerElementIndex--;
        // 倒数第二个情况是, smallerElmentIndex === biggerElementIndex，swap() 相同位置
        // 之后下一轮，只会满足两个 while 的其中一个，然后进入 break
        if(smallerElementIndex > biggerElementIndex) break;
        swap(array, smallerElementIndex, biggerElementIndex)
    // Now array[smallerElementIndex] is the first element bigger thant pivot
    swap(array, smallElementIndex, right)
    return smallerElementIndex

代码​

public void quickSort(int[] array, int left, int right) {
    if (left >= right) return ;
    int partitionIndex = partition(array, left, right);
    quickSort(aray, left, partitionIndex - 1);
    quickSort(array, partitionIndex + 1, right);
}

public int partition(int[] array, int left, int right) {
    int pivot = array[right];
    int leftIndex = left;
    int rightIndex = right - 1;
    while (true) {
        while (leftIndex < right && array[leftIndex] <= pivot) {
            leftIndex++;
        }
        while (rightIndex >= left && array[rightIndex] > pivot) {
            rightIndex--;
        }
        if (leftIndex > rightIndex) {
            break;
        }
        swap(array, leftIndex, rightIndex);
    }
    swap(array, lefIndex, right); //swap pivot to the right position
    return leftIndex;
}

public void swap (int[] array, int left, int right) {
    int temp = array[left];
    array[left] = array[right];
    array[right] = temp;
}

复杂度分析​

info

每层为 n, logN 层

时间复杂度: O(n^2)，平均时间复杂度: O(nlogN)
空间复杂度: O(n)，平均时间复杂度: O(logN) // 分层分成 n 层占用的空间

归并排序 Merge Sort​

在此算法中，我们将一个数组分为两个子数组，通过递归重复将数组切分到只剩下一个元素为止。然后将子数组中的元素排序后合并，通过不断合并子数组，最后就会拿到一个排好序的大数组。

归并排序和快排一样，也是一种分而治之 (Divide and Conquer) 算法。简单理解为将大问题变为小问题，然后把所有小问题都解决掉，大问题就迎刃而解。其中主要包括两个步骤：

  1. 切分步骤：将大问题编程小问题，通过递归解决更小的子问题。
  2. 解决步骤：将小问题的结果合并，以此找到大问题的答案。

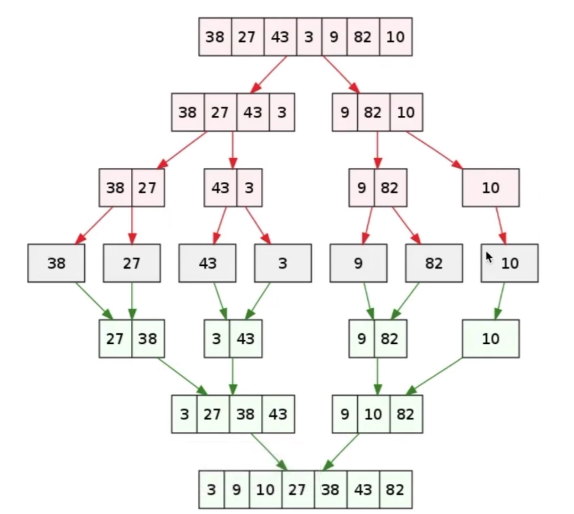
High Level Think​

  1. 递归切分当前数组
  2. 如果当前数组数量小于等于 1，无需排序，直接返回结果。
  3. 否则将当前数组分为两个子数组，递归排序这两个子数组
  4. 在子数组排序结束后，将子数组的结果归并成排好序的数组
Pseudocode
function mergeSort(array[], start, end):
    if (end - start < 1) return; // 无需排序，直接返回结果
    mid = (start + end) / 2
    mergeSort(array, start, mid)
    mergeSort(array, mid + 1, end)
    merge(array, start, mid, end)

function merge(array, start, mid, end) {
    helper[] = array.copy()
    leftStart = start, rightStart = mid + 1;
    while (leftStart <= mid || rightStart <= end):
        if (helper[leftStart] <= helper[rightStart]):
            array[start++] = helper[leftStart++]
        else:
            array[start++] = helper[rightStart++]
    if (leftStart <= mid):
        while (leftStart <= mid):
            array[start++] = helper[leftStart++]
    else:
        while (rightStart <= end):
            array[start++] = helper[rightStart++]
}
tip

切分并不是真的复制很多个数组，而是通过切分，知道我们应该取当前数组的哪个 index 作为 start, 哪个 index 作为 end，计算出需要用在 merge 的参数 mid。
拿上图为例，如果我们切分出 [38, 27] 的子数组去做切分，我们会得到 start=0, mid=0, end=1 的情况，我们在使用 merge([38, 27], 0, 0, 1) 去合并得到 [27, 38] 的排序结果。

代码​

public void mergeSortAlgorithm(int[] array) {
    int[] helper = copy(array);
    mergeSort(array, helper, 0, array.length -1);
    return array;
}

public void mergeSort(int[] array, int[] helper, int left, int right) {
    if (right - left < 1) return;
    int mid = left + (right - left) / 2;
    mergeSort(array, helper, left, mid);
    mergeSort(array, helper, mid+1, right);
    merge(array, helper, left, mid, right);
}

public void merge(int[] array, int[] helper, int left, int mid, int right) {
    for (int i = left; i <= right; i++) {
        helper[i] = array[i];
    }
    int leftStart = left;
    int rightStart = mid + 1;
    for(int i = left; i <= right; i++) {
        if(leftStart > mid) {
            array[i] = helper[rightStart++];
        } else if (rightStart > right) {
            array[i] = helper[leftStart++];
        } else if (helper[leftStart] <= helper[rightStart]) {
            array[i] = helper[leftStart++];
        } else {
            array[i] = helper[rightStart++];
        }
    }
}

复杂度分析​

时间复杂度: O(nlogN)
空间复杂度: O(n) // helper 数组占用空间 n

时间空间复杂度对比​

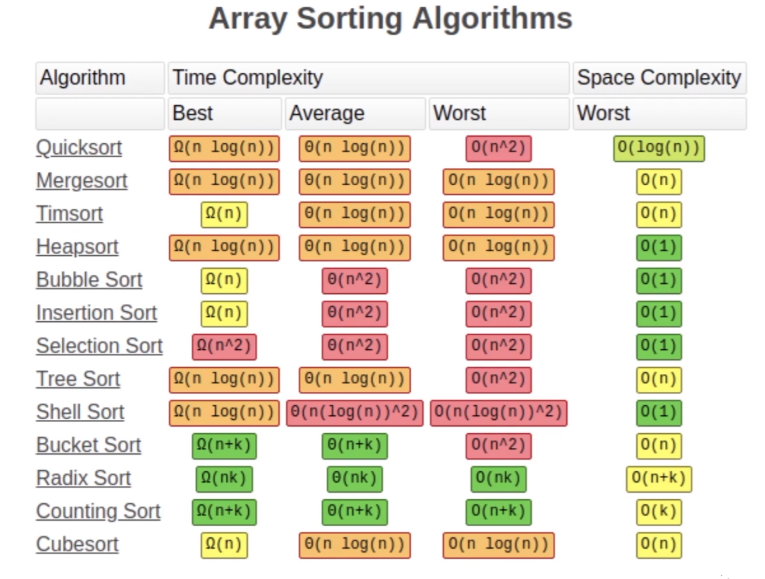
来源​