Skip to main content

Binary Search 搜索

Binary Search 定义​

一种针对有序区间内的 o(logN) 搜索方式，最常见用于已经排好序的 Array。

Binary Search 两大基本原则​

  1. 每次都要缩减搜索区域。Shrink the search space every iteration (or recursion)
  2. 每次缩减不能排除潜在答案。Cannot exclude potential answers during each shrinking

Binary Serach 三大模版 (三种变种)​

找一个准确值​

  • 循环条件 l <= r
  • 缩减搜索空间: l = mid + 1, r = mid -1
// 找一个精确值
public int binarySearch(int[] arr, int k) {
    int l = 0, r = arr.length -1;

    while (l <= r) {
        // int mid = (l + r) / 2 // Has possibility exceeds maximum limit
        int mid = l + (r - l) / 2;
        if (arr[mid] == k) {
            return mid;
        } else if (arr[mid] > k) {
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }

    return -1;
}

找一个模糊值(比 4 大的最小数)​

  • 循环条件: l < r (最终得到 l, r 是同一个值, l = r 会进一步运行程序体)
  • 缩减搜索空间: l = mid, r = mid -1 或者 l = mid + 1, r = mid

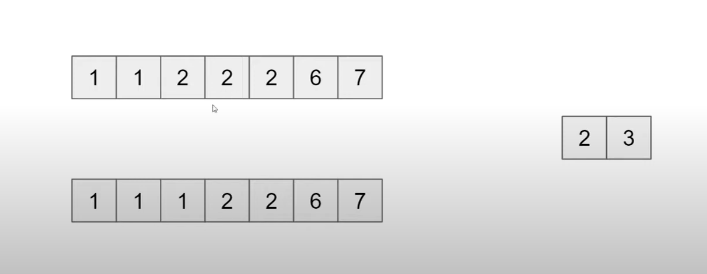
例题(First Occurance of 2)​

  • 循环条件: l < r (不等于是为了避免死循环)
  • mid = l + (r - l) / 2
  • 缩减搜索空间: l = mid + 1, r = mid

public int binarySearch(int[] arr, int k) {
    int l = 0, r = arr.length - 1;
    while (l < r) {
        int mid = l + (r - l) / 2;
        if (arr[mid] < k) {
            l = mid +1;
        } else {
            r = mid;
        }
    }
}

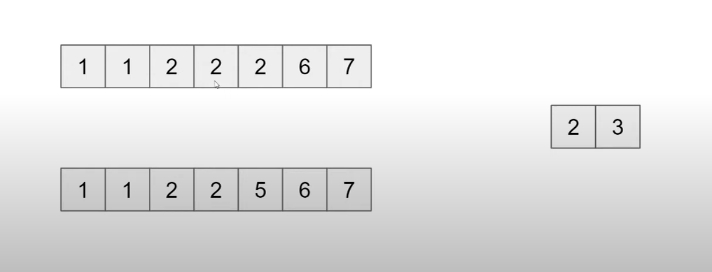
例题(Last Occurance of 2)​

  • 循环条件: l < r (最终得到 l, r 是同一个值，但 l = r 并不会进一步运行程序体)
    • mid = l + (r - l + 1) / 2
  • 缩减搜索空间: l = mid, r = mid - 1

public int binarySearch(int[] arr, int k) {
    int l = 0, r = arr.length -1;
    while (l < r) {
        int mid = l + (r - l + 1 ) / 2; // 当遇到[2, 3], l = 2, r = 3, 的情况下，需要 mid = 3 停在右边, 所以这里需要针对偶数个数组情况额外 + 1
        if (arr[mid] > k) {
            r = mid - 1;
        } else {
            l = mid;
        }
    }
}

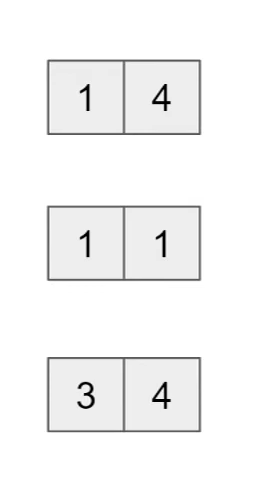
万用型 (Closest to 2)​

  • 循环条件: l < r - 1 (最终得到 l, r 两个相邻的值，得到相邻之前运行的程序体缩减范围后会得出两个 l, r 值)
  • 缩减搜索空间: l = mid, r = mid

public int binarySearch(int[] arr, int k) {
    int l = 0, r = arr.length-1;
    while (l < r - 1) {
        int mid = l + (r - l) / 2;
        if (arr[mid] < k) {
            l = mid;
        } else {
            r = mid;
        }
    }

    if (arr[r] < k) {
        return r;
    } else if (arr[l] > k) {
        return l
    } else {
        return k - arr[l] < arr[r] - k ? l : r;
    }
}

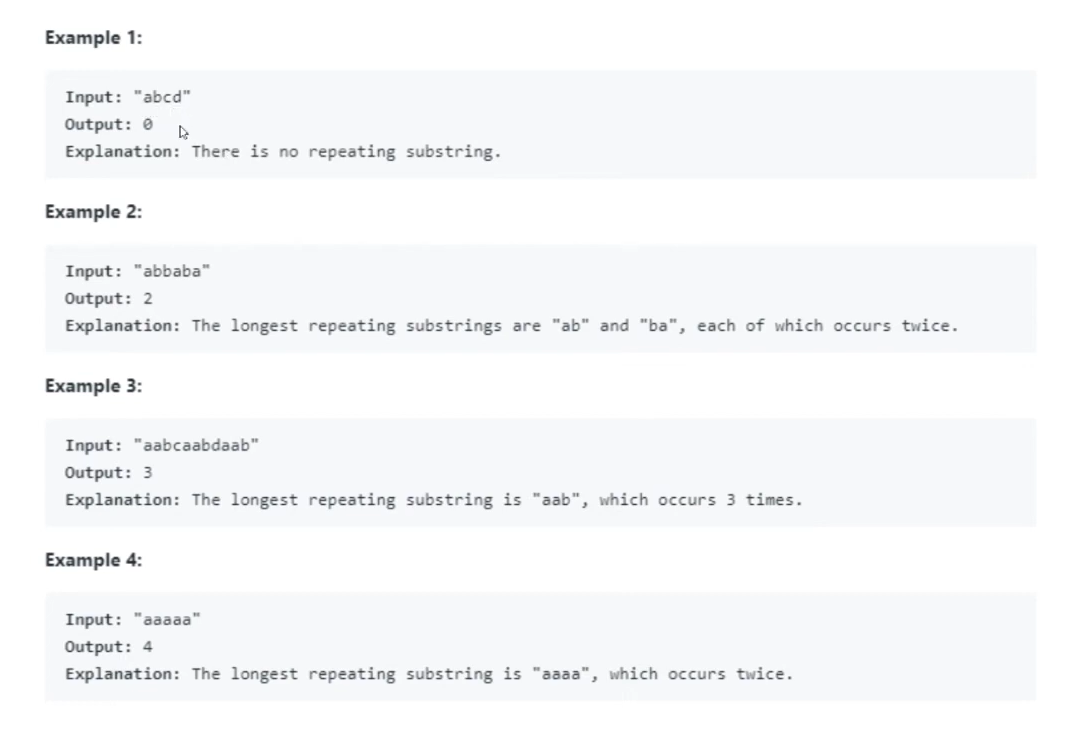
有序区间 1062 Longest Repeating Substring​

Given a string s, find out the length of the longest repeating substring(s). Return 0 if no repeating substring exists.

public int longestRepeatingSubstring(String s) {
    int l = 0, r = s.length() - 1;
    while (l < r) {
        int mid = l + (r - l + 1) / 2; // mid: 重复字符串的长度
        if (f(s, mid)) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}
// f(x): Verify if length x is a valid answer for the LRS (Longest Repeating Substring)
public boolean f(String s, int length) {
    Set<String> seen = new HashSet<>();
    for (int i = 0; i <= s.length() - length; i++) { // 按照 length 长度去 loop 整个字符串, 我们要避免 loop 超过 字符串长度 -> s.length() - length
        int j = i + length  - 1; // 从 i 开始, 取 length 长度的字符串
        String sub = s.substring(i, j + 1); // 通过 + 1 取出 [i, j]
        if (seen.contains(sub)) { // 判断 s 字符串中, length 长度的字符串是否重复
            return true;
        }
        seen.add(sub);
    }
    return false;
}

更多例题​

  • Aplit Array Largest Sum (410) -> Done
  • Divide Chocolate (1231)
  • Peak Index in a Mountain Array (852) -> Done
  • Capacity To Ship Packages Within D Days (1011) -> Done
  • Maximum Side Length of a Square with Sum Less than or Equal to Threshold (1292) -> Done

来源​