Sorting
What is sorting?
Sorting is any process of arranging items systematically. In computer science, sorting algorithms put elements of a list in a certain order.
The most frequently used orders are numerical (according to numbers) and lexicographical (according to letters). Efficient sorting is important for optimizing the efficiency of other algorithms, which require sorted input or the sort of a given input as part of their process.
Formal definition
A list or array is sorted in ascending order if ∀i, such that i≤n−1, A[i]≤A[i+1]. Similarly, a list or array is sorted in descending order if ∀i, such that i≤n−1, A[i]≥A[i+1].
Sorting Algorithms
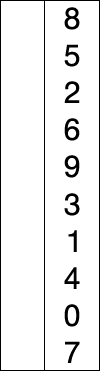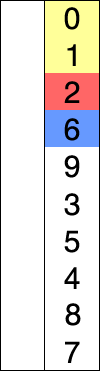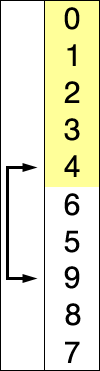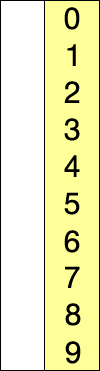
Selection sort
This algorithm works by repeatedly finding the minimum element in the list and placing it at the beginning. This way, the algorithm maintains two lists:
- the sublist of already-sorted elements, which is filled from left to right
- the sublist of the remaining unsorted elements that need to be sorted
In other words, this algorithm works by iterating over the list and swapping each element with the minimum (or maximum) element found in the unsorted list with that in the sorted list.
def selection_sort(lst):
for i in range(len(lst)):
min_index = i
for j in range(i + 1, len(lst)):
if lst[min_index] > lst[j]:
min_index = j
lst[i], lst[min_index] = lst[min_index], lst[i]
# lst[j], lst[min_index] = lst[min_index], lst[j] # @Wrong: j is the iterate position, but the position to fill. we should freeze fill possition as i
return lst
# Driver code to test above
if __name__ == "__main__":
lst = [3, 2, 1, 5, 4]
selection_sort(lst) # Calling selection sort function
# Printing Sorted lst
print("Sorted lst: ", lst)
Complexity
- Time complexity:
O(n^2) - Space complexity:
O(1)
Bubble sort
This is another famous sorting algorithm also known as ‘sinking sort’. It works by comparing adjacent pairs of elements and swapping them if they are in the wrong order. This is repeated until the list is sorted.
Think of it this way: a bubble passes over the list, ‘catches’ the maximum/minimum element, and brings it over to the right side.
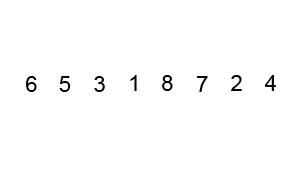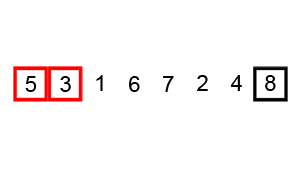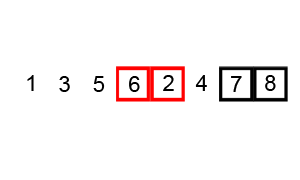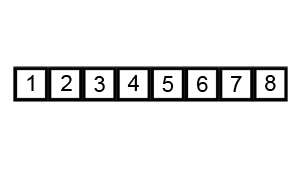
def bubble_sort(lst):
for i in range(len(lst)): # here one loop to get one results in list
for j in range(
len(lst) - 1 - i # last i elements are already in place
): # Here loop from first element to second last element and do the bubble check
if lst[j] > lst[j + 1]:
lst[j], lst[j + 1] = lst[j + 1], lst[j]
return lst
# Driver code to test above
if __name__ == "__main__":
lst = [3, 2, 1, 5, 4]
bubble_sort(lst) # Calling bubble sort function
print("Sorted list is: ", lst)
Complexity
- Time complexity:
O(n^2) - Space complexity:
O(1)
Insertion sort
Insertion sort is another famous sorting algorithm and works the way you would naturally sort in real life.
It iterates over the given list, figures out what the correct position of every element is, and inserts it there.
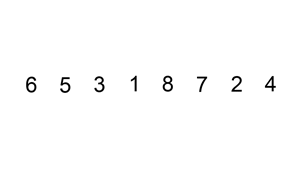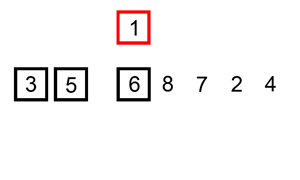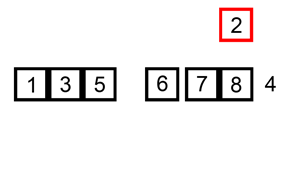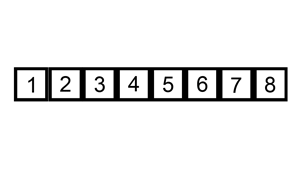
def insertion_sort(lst):
for i in range(1, len(lst)):
key = lst[i]
# Move elements of lst greater than key, to one position ahead
j = i - 1
while j >= 0 and key < lst[j]:
lst[j + 1] = lst[j]
j -= 1
lst[j + 1] = key
return lst
# Driver code to test above
if __name__ == "__main__":
lst = [3, 2, 1, 5, 4]
insertion_sort(lst) # Calling insertion sort function
print("Sorted list is: ", lst)
Complexity
- Time complexity:
O(n^2) - Space complexity:
O(1)
Merge sort
Merge sort is a recursive divide & conquer algorithm that essentially divides a given list into two halves, sorts those halves, and merges them in order. The base case is to merge two lists of size 1 so, eventually, single elements are merged in order; the merge part is where most of the heavy lifting happens.
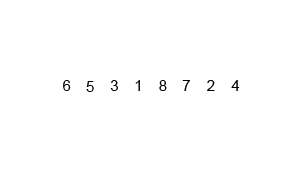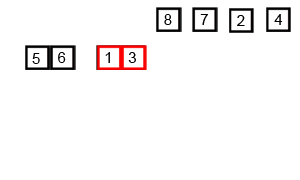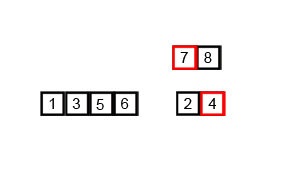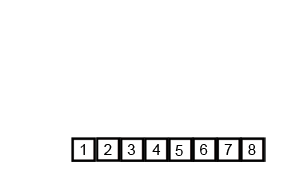
def merge_sort(lst):
if (
len(lst) > 1
): # At least with a list with two elements to make sure sub merge_sorts trigger correctly
mid = len(lst) // 2
left = lst[:mid]
right = lst[mid:]
print("mid", mid)
print("left", left)
print("right", right)
merge_sort(left)
merge_sort(right)
i = 0
j = 0
k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
lst[k] = left[i]
i += 1
else:
lst[k] = right[j]
j += 1
k += 1
while i < len(left):
lst[k] = left[i]
i += 1
k += 1
while j < len(right):
lst[k] = right[j]
j += 1
k += 1
return lst
# Driver code to test the above code
if __name__ == "__main__":
lst = [3, 2, 1, 5, 4]
merge_sort(lst)
print("Sorted list is: ", lst)
Complexity
- Time complexity:
O(nlog(n))
Quick sort
Quick sort is the fastest-known, comparison-based sorting algorithm for lists in the average case.
Steps for quick sort algorithm
- Start with a list of n elements
- Choose a pivot element from the list to be sorted
- Partition the list into 2 unsorted sublists, such that all elements in one sublist are less than the pivot and all the elements in the other sublist are greater than the pivot
- Elements that are equal to the pivot can go in either sublist
- Sort each sublist recursively to yield two sorted sublists
- Concatenate the two sorted sublists and the pivot to yield one sorted list
def choose_pivot(left, right):
pass
def quick_sort(lst, left, right):
pass
# Driver code to test above
if __name__ == "__main__":
lst = [5, 4, 2, 10, 1, 3, 6, 9]
quick_sort(lst, 0, len(lst) - 1)
# Printing Sorted list
print("Sorted list: ", lst)
Complexity
- Time complexity:
O(nlog(n)), worst-case time complexisty:O(n^2)
排序算法对比
Insertion sort vs Quick sort
- 都有 i, j, 对比值(i value, privot value), Insertion sort 中 i 是对比值的位置,j 负责移动 check 和 fill,并且 j 是从 i-1(或 i) 的位置往 0 移动; Quick sort 中 privot value 是对比值,位于 right 位置,i 负责 fill, j 负责移动 check,并且 j 从 i 的位置往 right 移动。
Merge sort vs Quick sort
- Merge sort 先拆分在排序,核心逻辑是如何把两个 lst 合并为一个。
- Quick sort 是在拆分中排序,核心逻辑是找到 privot 然后围绕 privot 对数据做区分 partition。