Algorithmic Paradigms
Brute Force
Definition
This method requires us to go through all the possibilities to find a solution to the problem we want to solve.
Example: linear search
def find_index(lst, key):
for i in range(len(lst)):
if lst[i] == key:
return i
return -1
if __name__ == "__main__":
number_to_search = 7
nums = [2, 4, 6, 3, 5, 7, 9, 1, 8]
print("Number", number_to_search, "is at index", find_index(nums, number_to_search))
def maximum_index(lst):
max_index=-1
max_val = -99999
for i in range(leng(lst)):
if lst[i] > max_val:
max_val = lst[i]
max_index = i
return max_index
if __name__ == "__main__":
nums = [2, 4, 6, 3, 5, 7, 9, 1, 8]
max = maximum_index(nums)
print("Maximum number in the list is", nums[max], "at index ", max);
def minimum_index(lst):
min_index = -1
min_val = 9999
for i in range(len(lst)):
if min_val > lst[i]:
min_val = lst[i]
min_index = i
return min_index
if __name__ == '__main__':
nums = [2, 4, 6, 3, 5, 7, 9, 1, 8]
min = minimum_index(nums)
print("Minimum number in the list is", nums[min], "at index ", min)
Advantages
The good thing about the Brute Force method is that, if a solution to our problem exists, we are guaranteed to find the solution this way.
Disadvantages
It is the most inefficient one. Also, there are no shortcuts and no performance improvements at this stage.
Greedy Algorithms
Definition
Recursion is an approach to problem-solving in which the solution to a particular problem depends on solutions to smaller instances of the same problem.
The Greedy method can solve a problem that satisfies the below-mentioned properties:
- Greedy choice property: A global optimum can be arrived at by selecting a local optimum.
- Optimal substructure: An optimal solution to the complete problem contains an optimal solution to subproblems.
Greedy algorithms work by recursively constructing a set of pieces from the smallest possible constituent parts.
Example
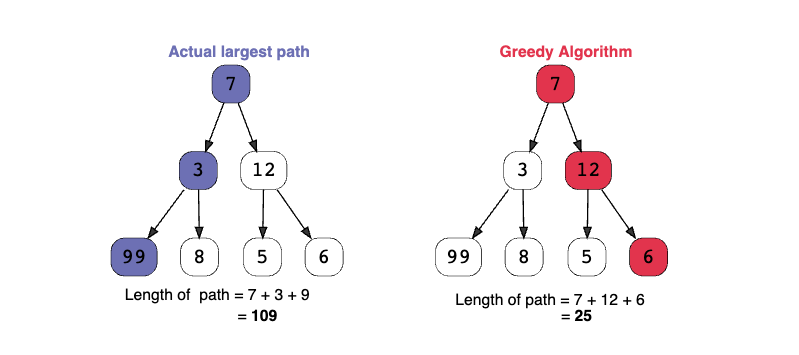
Advantages
The advantage of using a greedy algorithm is that solutions to smaller instances of the problem can be straightforward and easy to understand. Also, it works in some cases, especially where the optimal solution of the subset is the solution for the superset as well.
Disadvantages
The disadvantage of the greedy algorithm is that sometimes the most optimal short-term solutions may lead to the worst possible solution to the whole problem!
Divide and Conquer
Definition
Divide and conquer is an algorithmic paradigm in which the problem is repeatedly divided into subproblems until we reach a point where each problem is similar and atomic (i.e., can’t be further divided).
3 steps
- Divide First, break the problem at hand into smaller subproblems. This step can be achieved by dividing the list containing the alphabets into sublists until a single unit is left and no further division is possible.
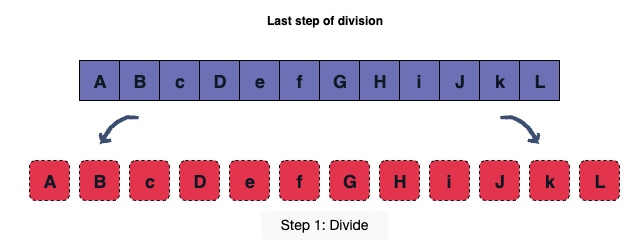
- Conquer Solve the received atomic subproblems from step 1. Often, the problems are considered solved and passed onto the next step.

- Merge Repeatedly combine the solved subproblems to formulate a solution for the original problem.

Advantages
- It can be optimal for a general case solution where the problem is easy to divide, and the subproblem at some level is easy to solve.
- It makes efficient use of memory cache because, when the problem gets divided into subproblems, it becomes smaller enough to be easily solved in the cache itself.
Disadvantages
- It uses a recursive approach and the most common issue with recursion is that it is slow. Sometimes, it can be more complicated than a basic iterative approach, especially in cases with a large n.
For example, adding multiple numbers using a simple loop is much simpler and efficient than dividing the numbers into two groups, adding these groups recursively, and then adding the sums of the two groups. - Since the problem is solved using recursion, it may end up duplicating some subproblems and lead to huge recursive stacks, which consequently consumes extra space.
Dynamic Programming
Definition
Dynamic programming algorithms solve problems by combining results of subproblems — just like divide and conquer algorithms.
Characteristics
- Overlapping Subproblems: the subproblems of a given problem are not independent. In other words, two subproblems share a problem.
- Optimal Substructure Property: the overall optimal solution of the problem can be constructed from the optimal solutions of its subproblems.
Dynamic programming patterns
Memorization (top - down)
The memoized version of a problem is similar to the regular recursive version, except that it looks for the answer of a subproblem in a lookup table before computing its solution.
-f82f352e82dc8df5a96e7b1d697bba3d.png)
Tabulation (bottom - up)
Tabulation is the opposite of the top-down approach and it avoids recursion. In this approach, we solve the problem “bottom-up”. This is typically done by filling up a lookup table and computing the solution to the top/original problem based on the results in the table.
-fef9563ca0c26a6d0441390d3115c553.png)
Advantages
- Being a recursive programming technique, it reduces the lines of code.
- It speeds up the processing, as we use the answer of a previously-calculated subproblem to get the next one.
Disadvantages
- It takes a lot of memory to store the calculated result of every subproblem without ensuring if the stored value will be utilized or not, which leads to unnecessary memory utilization.
- There is no general form for problems solved by dynamic programming, i.e., every problem has to be solved in its own way.
3 种算法范式对比
三大算法对比总表
| 特性 | 贪心算法(Greedy) | 分治算法(Divide & Conquer) | 动态规划(DP) |
|---|---|---|---|
| 核心思想 | 每一步选择当前局部最优解,希望组合成全局最优。 | 将问题分解为独立子问题,递归解决后合并结果。 | 分解为重叠子问题,存储子问题解避免重复计算。 |
| 子问题性质 | 无重叠,但选择会影响后续决策。 | 子问题独立无重叠。 | 子问题重叠且需重复计算。 |
| 最优性保证 | 不保证全局最优(需证明贪心选择性质)。 | 保证全局最优(子问题解正确合并)。 | 保证全局最优(存储子问题解)。 |
| 存储子问题解 | 不存储,直接做出选择。 | 不存储,每次递归重新计算。 | 必须存储(记忆化或表格)。 |
| 时间复杂度 | 通常最低(如 O(n) 或 O(n log n))。 | 中等(如归并排序 O(n log n))。 | 较高(如背包问题 O(nW))。 |
| 空间复杂度 | 通常 O(1) 或 O(n)。 | 取决于递归深度(如快速排序 O(log n))。 | 需额外存储空间(如 O(n²))。 |
| 适用条件 | 问题具有贪心选择性质(如活动选择)。 | 问题可拆分为独立子问题(如排序)。 | 问题具有重叠子问题和最优子结构(如斐波那契、LCS)。 |
| 经典问题 | 霍夫曼编码、Dijkstra 最短路径。 | 归并排序、快速排序、大整数乘法。 | 背包问题、最长公共子序列(LCS)、编辑距离。 |
优缺点总结
| 算法 | 优点 | 缺点 |
|---|---|---|
| 贪心算法 | 1. 高效,时间复杂度低。 2. 实现简单。 | 1. 不保证全局最优。 2. 需严格证明贪心选择性质。 |
| 分治算法 | 1. 逻辑清晰,易于理解。 2. 适合并行计算(子问题独立)。 | 1. 递归开销大。 2. 不适用于重叠子问题。 |
| 动态规划 | 1. 保证全局最优解。 2. 可解决复杂重叠子问题。 | 1. 时间和空间复杂度高。 2. 需要设计状态转移方程。 |
一句话总结
- 贪心:“眼前最优,不管未来。” (简单高效,但需证明正确性。)
- 分治:“分而治之,各自为政。” (适合独立子问题,但递归成本高。)
- DP:“记住历史,避免重复。” (通用但复杂,空间换时间。)