动态规划 Dynamic Programming

Most problems that can be solved with dynamic programming can also be solved with a divide and conquer approach. The difference between the two is that the dynamic programming approach is applicable when a problem has overlapping subproblems;

Furthermore, dynamic programming problems have the optimal substructure property, which means that the overall optimal solution of the problem can be constructed from the optimal solutions of its subproblems.

Dynamic programming algorithms solve every subproblem just once and save the answer in a lookup table, thereby avoiding recalculating the answer every time the subproblem is encountered.

Dynamic programming Patterns

There are two dynamic programming patterns: memoization and tabulation.

Memoization (top-down)

The memoized version (yes, that is not a typo - it’s memoization not memorization) of a problem is similar to the regular recursive version; the difference is that it looks for the answer of a subproblem in a lookup table before computing its solution. If the precomputed value exists, then it is returned. Otherwise, the value is computed and put in the lookup table so that it can be reused later.

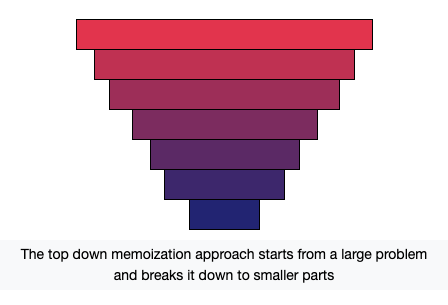
Tabulation (bottom-up)

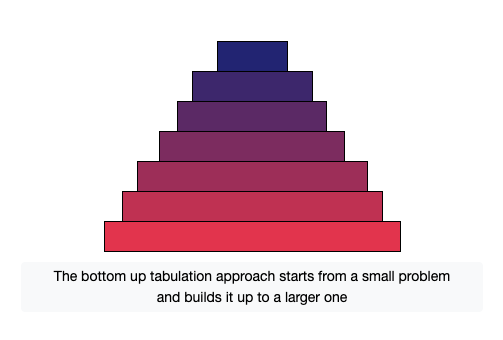
Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related subproblems first). This is typically done by filling up a lookup table and based on the results in the table, the solution to the top/original problem is then computed.

DP 解题思路

• DP 数组以及下标含义
• 递推公式
• DP 数组如何初始化
• 遍历顺序
• 打印 DP 数组 (Debug)

基本题型

• 背包问题
• 打家劫舍
• 股票问题
• 子序列问题

Calculating Fibonacci Numbers

非动态规划解法

def fib(num):
    """
    Finds nth fibonacci number
    :param num: An integer number
    :return: nth fibonacci number
    """
    if num <=1:
        return num
    return fib(num-1) + fib(num-2)

# Driver code to test above function
if __name__ == '__main__':
  num = 6
  print(fib(6))

这个解法的问题是，有非常多重复计算的子问题。

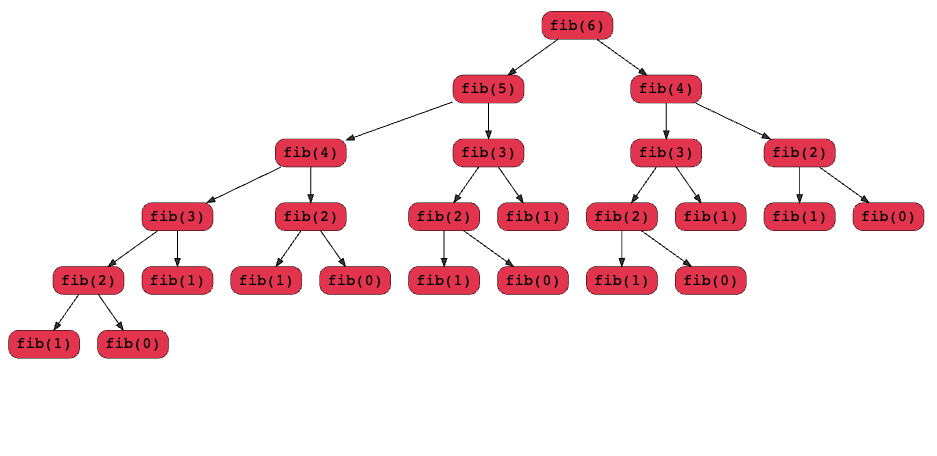
Complexity

• Time complexity: O(2^n)

动态规划解 记忆法 Memoized

def fib (num, lookup_table):
    """
    Finds nth fibonacci number
    :param num: An integer number
    :param lookup_table: Stores already calculated fibonacci number
    :return: nth fibonacci number
    """
    if lookup_table[num] == -1: # Check if already present

        # Adding entry to table when not present
        if num<=1:
            lookup_table[num] = num
        else:
            lookup_table[num] = fib(num-1, lookup_table) + fib(num-2, lookup_table)

    return lookup_table[num]

# Driver code to test above function
if __name__ == "__main__":
    num = 6 # Finding the nth Fibonacci number
    lookup_table = [-1] * [num + 1] # Initializing the lookup table to have -1 of size num + 1
    print(fib(num, lookup_table))

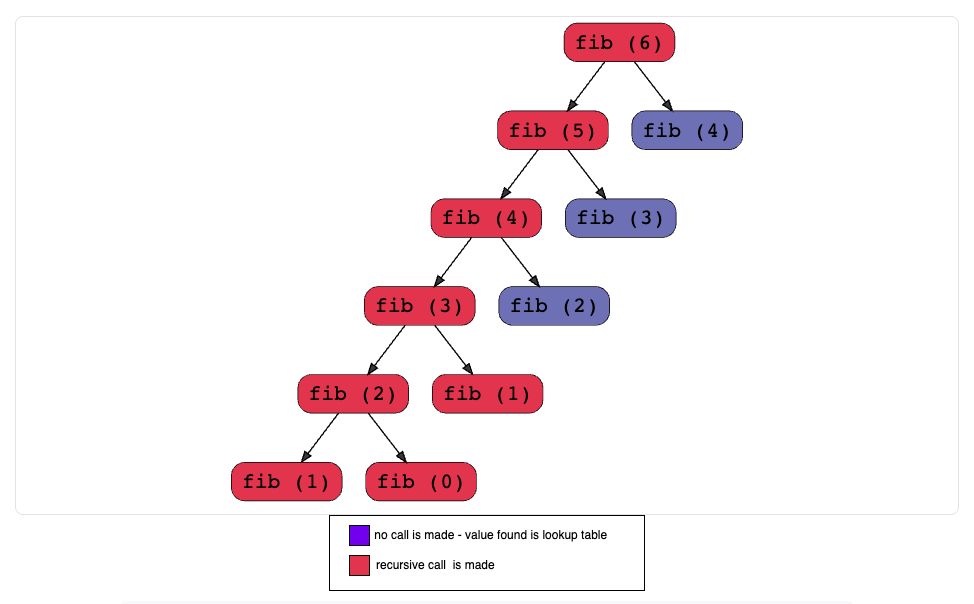
Complexity

• Time complexity: O(n)
• Space complexity: O(n)

动态规划解 制表法 Tabulated

def fib (num, lookup_table):
    """
    Finds nth fibonacci number
    :param num: An integer number
    :param lookup_table: Stores already calculated fibonacci number
    :return: nth fibonacci number
    """
    # Set 0th and first values
    lookup_table[0]=0
    lookup_table[1]=1

    for i in rage(2, num + 1):
        # Fill up the table by summing up previous two values
        lookup_table[i] = lookup_table[i-2] + lookup_table[i-1]

    return lookup_table[num] # Return the nth Fibonacci number

# Driver code to test above function
if __name__ == "__main__":
    num = 6 # Finding the nth Fibonacci number
    lookup_table = [0] * [num + 1] # Initializing the lookup table to have 0 of size num + 1
    print(fib(num, lookup_table))

Complexity

• Time complexity: O(n)
• Space complexity: O(n)

动态规划 制表法 Tabulated (优化空间复杂度)

def fib(num):
    """
    Finds nth fibonacci number
    :param num: An integer number
    :return: nth fibonacci number
    """
    # Base case
    if num <= 1:
        return num

    second_last = 0 # The 0th
    last = 1 # The first
    current = 0

    for i in range(2, num+1):
        # current is the sum of the last plus second last number before the current one
        current, second_last = second_last + last, last
        last = current

    return current

# Driver code to test above function
if __name__ == '__main__':
    num = 6
    print(fib(num))

Complexity

• Time complexity: O(n)
• Space complexity: O(1)