Skip to main content

Transformer 架构

模型架构​

encoder-decoder 架构

  • 输入一个长为 n 的输入序列(x1,...,xn)，编码器 encoder 会将它翻译为一个长为 n 的 (z1,...,zn) 的机器学习可以理解的向量序列
  • 解码器 decoder 拿到 (z1,...,zn) 并生成一个长为 m 的 (y1,...,ym), 解码器里面只能一个一个的生成 (自回归模型 auto-regressive model,你的输入也是你的输出)

Transformer 的特点: multi-head self-attention mechanism and point-wise fully connected feed-forward network for both encoder and decoder.

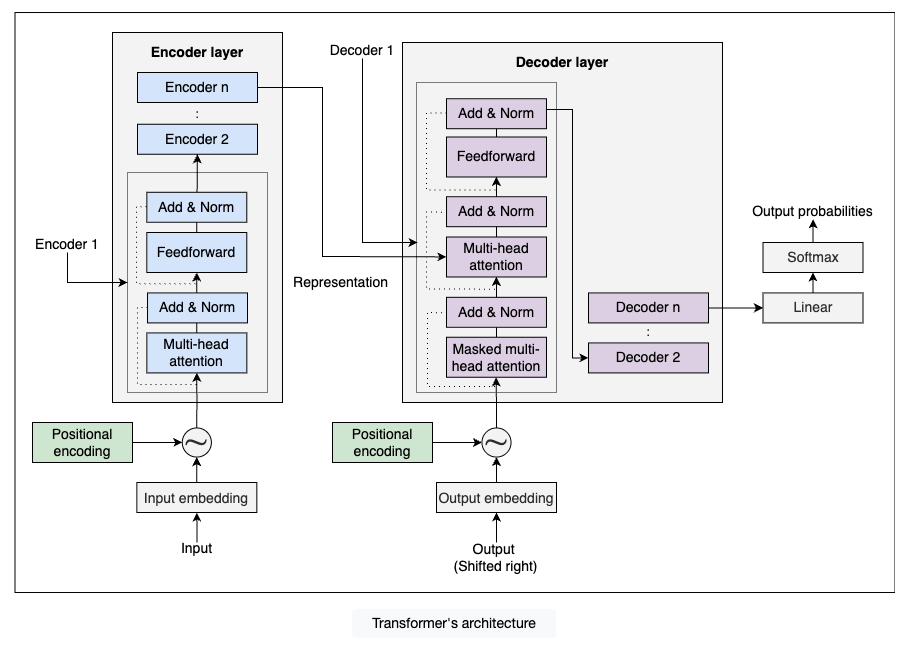
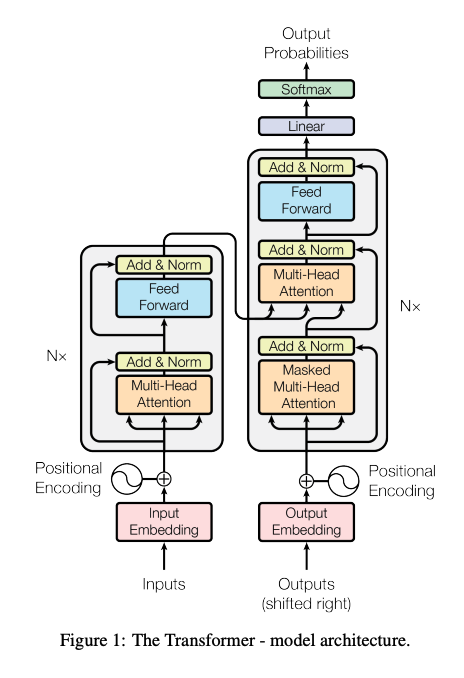
编码器和解码器​

编码器​

编码器有 n=6 层，每层有两个子层(分别是 multihead self-attention mechanism 和 feedforward network)。每个子层有分别增加了一个 residual conenction 残差连接 和 一个 normalization 层。

数学表示:

LayerNorm(x+Sublayer(x))

  • x: 是 input
  • x + Sublayer(x) 是残差连接
  • 为方便计算残差，所有 sub-layers 的输出长度统一为 d(model)= 512

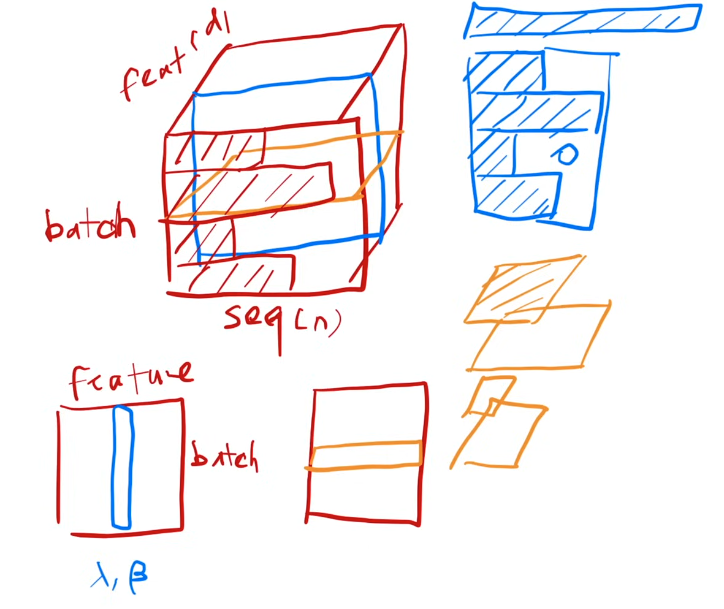
BatchNorm vs LayerNorm

解码器​

解码器器有 n =6 层，每层有两个子层(分别是 multihead self-attention mechanism 和 feedforward network)和 第三个子层同样是一个 masked multihead self-attention mechanism, 带有掩码，保证你 T 时间输出时是不会看到 T 时间之后的输入。

注意力层 Attention​

有两种注意力机制，一种叫 additive attention(可处理 query 和 key 不等长的情况)，另外一个叫点积注意力机制。

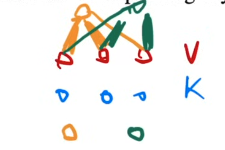
Transformer 中使用的注意力机制

Attention(Q,K,V)=softmax(QKTdk)VAttention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V

与正常的点积注意力机制相比，Transformer 的点积函数中加入了一个

1dk\frac{1}{\sqrt{dk}}

当你的 dk 不大的时候，你除不除都没关系，但是当你的 dk 比较大的时候，也就是说两个向量长度比较长的时候，你做点积的时候的值可能比较大或比较小；这些值做了 softmax 后，你会获得向两端更靠拢的值。这时算梯度的时候会比较小，导致跑不动。

这里这么做是因为 这里 dk=512, 所以除以 根号dk 是个不错的选择。

  • Q: 可以是多个 query, 可以是一个矩阵。
  • Q 和 K: 必须有相同的长度 dk。
  • K 和 V: 有相同 m 个，因为它们是键值对。

通过两次矩阵累积乘法来实现整个计算，另外矩阵累积乘法是很容易做并行的计算。

掩码层 Mask​

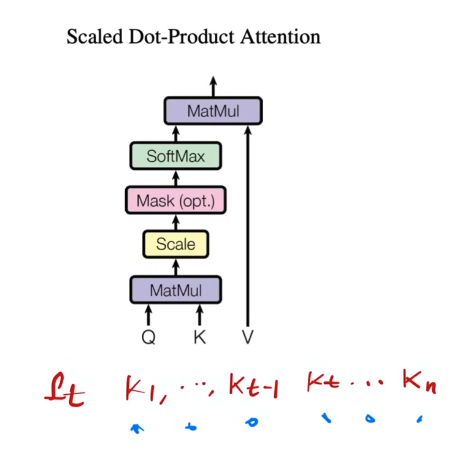
Mask 避免你在 dt 时间看到 dt 时间之后的东西。
Mask 会将 dt 之后的 kt 值(包括 kt) 换成一个 -1^10, 这个进入 SoftMax 计算的时候会变成 0。

多头注意力机制 Multi-Head Attention​

将单个注意力函数(整个 query, key, value) 投影到低维投影 h 次，做 h 次注意力函数，然后每个函数输出并在一起，在投影回来得到最终输出。

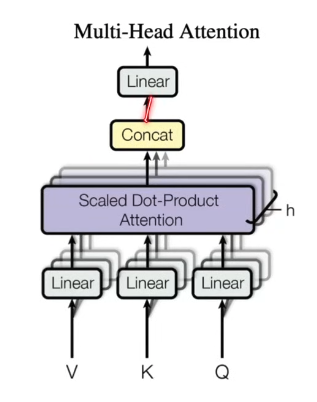
  • Linear: 投影到比较低的维度，投影的参数 w 是可以学的。
MultiHead(Q,K,V)=Concat(head1,...,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)MultiHead(Q, K, V) = Concat(head_1, ...,head_h)W^O \\ where\ head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)
  • i: 为一个批次
  • WQW^Q 是针对 Q 的投影参数, WKW^K 是针对 K 的投影参数, WVW^V 是针对 V 的投影参数。

论文里面，h = 8，因为有残差连接，你的输入和输出维度是一样的，之前设置的输出维度为 512。所以投影维度是

dk=dv=dmodel/h=64d_k=d_v=d_{model}/h=64

在 64 维计算注意力函数，然后再投影回来。

Transformer 中注意力机制的应用​

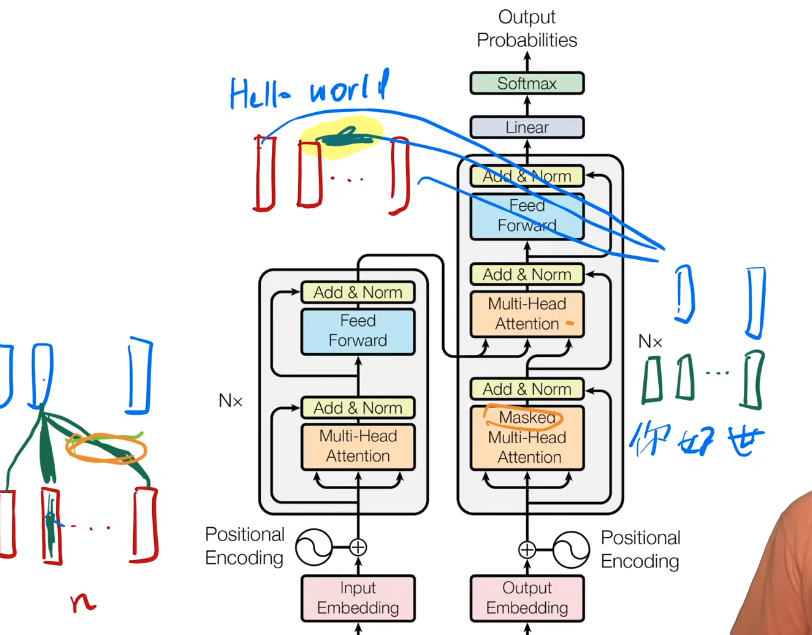
Transformer 的层状结构

Transformer 由多个堆叠的编码器层（Encoder Layers）和解码器层（Decoder Layers）组成。每一层的输入是前一层的输出：

  • 编码器：第 N 层（如第 2 层）的输入是第 N-1 层（如第 1 层）的输出。
  • 解码器：同理，解码器的每一层也接收前一层的输出作为输入。

这种堆叠方式允许模型逐层提取更高阶的特征（如从词法特征到句法、语义特征）。

具体场景中的“前一层的输出”

编码器的自注意力层（Self-Attention）

  • 输入来源：对于编码器的第 N 层，其 Q（查询）、K（键）、V（值）均来自同一位置——即前一层（第 N-1 层）的输出。
    • 例如，第 1 层的输入是词嵌入（Embedding），第 2 层的输入是第 1 层的输出，依此类推。
  • 作用：每个位置可以关注前一层的所有位置，捕捉上下文依赖。

解码器的自注意力层（Self-Attention）

  • 输入来源：与编码器类似，解码器的自注意力层的 Q/K/V 也来自前一层（解码器的第 N-1 层）。
    • 但为了保持自回归性质（不能看到未来信息），会通过掩码（Mask）限制当前位置只能关注之前的位置。

编码器-解码器注意力层（Cross-Attention）

  • 输入来源：
    • Q（查询）来自解码器前一层的输出。
    • K 和 V 来自编码器的最终输出（即编码器最后一层的输出）。
  • 作用：解码器通过 Q 查询编码器的信息（K/V），实现对齐输入序列和输出序列（类似传统 Seq2Seq 的注意力机制）。

Position-wise Feed-Forward Networks​

MLP apply to each position separately and identically.

FFN(x)=max(0,xW1+b1)W2+b2FFN(x)=max(0, xW_1+b_1)W_2+b_2

作用: 做语义空间的转换，对每个位置的表示进行非线性变换和特征增强。

Transformer MLP vs RNN MLP

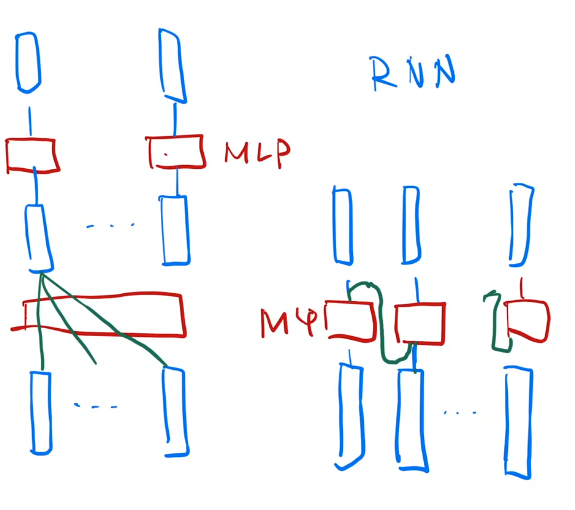
Embeddings and Softmax​

编码器输入，解码器输入，以及 Softmax 前的 linear 都有 Embeddings，这三个 Embeddings 有一样的权重。

另外，这些权重会乘一个 dmodel\sqrt{d_{model}}。原因: 避免学习 Embedding 时，向量维度大的时候，长度会变小，权重会变小。

Positional Encoding​

Attention 不会有时序信息，一段话相同的文字无论如何打乱，Attention 出现的结果都是一样的。

所以为了处理这个情况，我们用 Position Encoding 在输入里增加时序信息。

公式

PE(pos,2i)=sin(pos/100002i/dmodel)PE(pos,2i+1)=cos(pos/100002i/dmodel)PE_{(pos, 2i)}=sin(pos/10000^{2i/d_{model}}) \\ PE_{(pos, 2i+1)}=cos(pos/10000^{2i/d_{model}})

结果: [-1,1] 之间。

比如，请求嵌入层的信息是一个长为 512 的向量表示的，我的位置信息同样也可以是一个长为 512 的向量，向量的结果是由上面的公式计算所得，我只需要把这两个向量相加就可以把位置信息加入进去。

为了方便相加，所以上面 Embedding 的结果乘一个 dmodel\sqrt{d_{model}} 使每个数字也差不到在 [-1, 1] 的区域里面。

通过相加，位置信息会成为计算 quey 和 key 权重的因素之一而不仅仅是语义分析权重，影响权重信息，那么我在计算的时候应该考虑与当前位置信息相近的信息，从而确保顺序的正确性。

Why Self-Attention​

常用的是前三个，Self-Attention, Recurrent(RNN), Convolutional(CNN):

  • 它们三个的算法复杂度是差不多
  • Slef-Attention 和 Convolutional 计算上 (Sequential Operations) 会快一点
  • Self-Attention 在信息的糅合性 (Maxium Path Length) 上好一点

看上去 Attention 计算复杂度更好。
实际上，Attention 对模型假设更少，导致你需要更多的数据和更大的模型才能训练出与 RNN，CNN 获得同样效果。